Modern Evolutionary Biology

I. Population Genetics

A. Overview

Sources of Variation                                                Agents of Change
MUTATION:
-New Genes:                                                           Natural Selection
     point mutation                                                    Mutation (polyploidy can make new species)  

RECOMBINATION:
- New Genes:
    exon shuffling
-New Genotypes:
    -crossing over
    - independent assortment

In the early 20th century, at the same time that T. H. Morgan was studying mutations and creating linkage maps, other biologists were considering the evolutionary implications of this new knowledge regarding particulate, non-blending inheritance. They appreciated that individuals do not evolve - evolution is a process that occurs at the population level. For example, as a consequence of differential reproductive success among individuals in a population, the range of phenotypes and their relative frequencies in the population will change over time. Individuals are born, live, reproduce (maybe) and die. As a result of passing on their genes at different frequencies, the genetic structure of the population changes over time (evolution). Two biologists, G. Hardy and W. Weinberg, constructed a model to explain how the genetic structure of a population might change over time.

Their model begins by constructing an 'equilibrium' model - a model of what the genetic structure would look like, and how it would behave, if there was NO CHANGE over time. (We can liken this to a "statistical null hypothesis of no effect", right?). Then, an actual population is compared to this model, to see whether the population is evolving or not.    

B. The Genetic Structure of a Population

Our first step is to describe the genetic structure of a population; we need to do this before we can model what it would do over time. The genetic structure of a population is defined by the gene array and the genotypic array. To understand what these are, some definitions are necessary: 

1. Definitions:

                - Evolution: a change in the genetic structure of a population
                - Population: a group of interbreeding organisms that share a common gene pool; spatiotemporally and genetically defined
                - Gene Pool:  sum total of alleles held by individuals in a population
                - Genetic structure: Gene array and Genotypic array
                - Gene/Allele Frequency: % of alleles at a locus of a particular type
                - Gene Array: % of all alleles at a locus: must sum to 1.
                - Genotypic Frequency: % of individuals with a particular genotype
                - Genotypic Array: % of all genotypes for loci considered; must = 1.          

2. Basic Computations - Determining the Genotypic and Gene Arrays:

The easiest way to understand what these definitions represent is to work a problem showing how they are computed.               

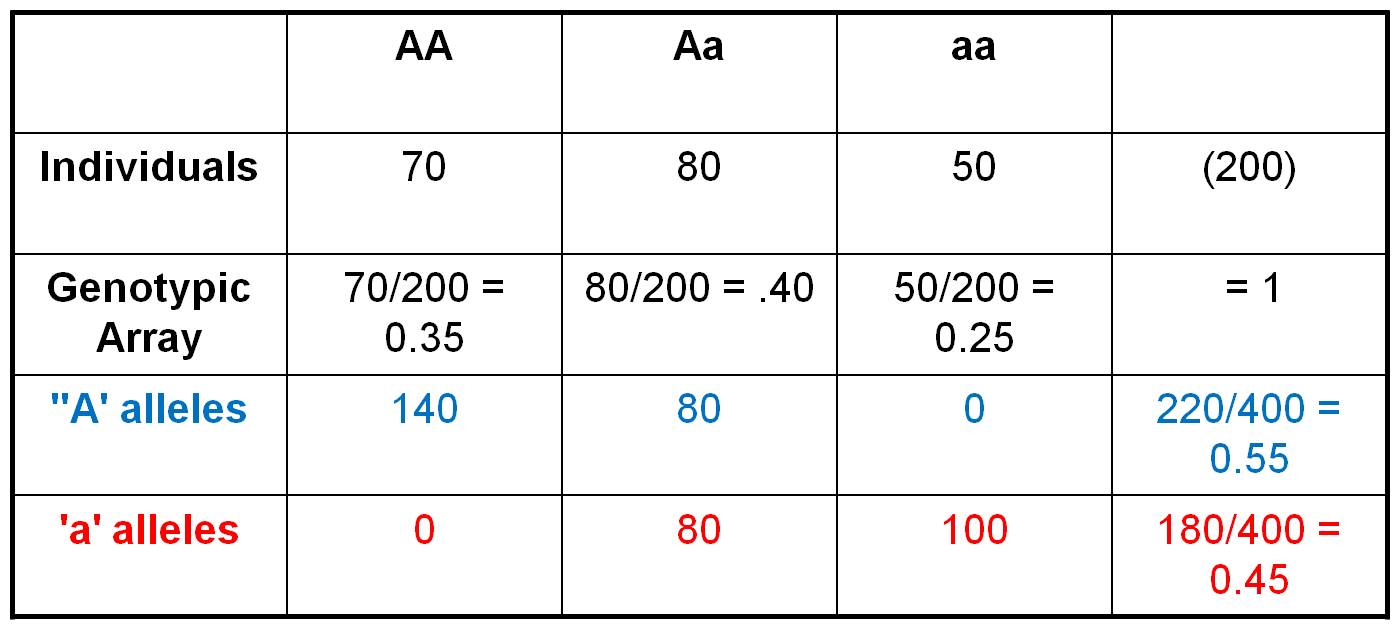
Consider the population shown to the right, in which there are 70 AA individuals, 80 heterozygotes, and 50 aa individuals. We can easily calculate the Genotypic Frequencies by dividing each of these values by the total number of individuals in the population. So, the Genotypic Frequency of AA = 70/200 = 0.35. If we account for all individuals in the population (and haven't made any careless math errors), then the three genotypic frequencies should sum to 1.0. The Genotypic Array would list all three genotypic frequencies: f(AA) = 0.35, f(Aa) = 0.40, f(aa) = 0.25. A Gene Frequency is the % of all genes in a population of a given type. This can be calculated two ways. First, let's do it the most obvious and direct way, by counting the alleles carried by each individual. So, there are 70 AA individuals. Each carries 2 'A' alleles, so collectively they are 'carrying' 140 'A' alleles. The 80 heterozygotes are each carrying 1 'A' allele. And of course, the 'aa' individuals aren't carrying any 'A' alleles. So, in total, there are 220 'A' alleles in the population. With 200 diploid individuals, there are a total of 400 alleles at this locus. So, the gene frequency of the 'A' gene = f(A) = 220/400 = 0.55. We can calculate the frequency of the 'a' alleles the same way. The 50 'aa' individuals are carrying 2 'a' alleles each, for a total of 100 'a' alleles. The 80 heterozygotes are each carrying an 'a' allele, and the 140 AA homozygotes aren't carrying any 'a' alleles. So, in total, there are 180 'a' alleles out of a total of 400, for a gene frequency f(a) = 180/400 = 0.45. The gene array presents all the gene frequencies, as: f(A) = 0.55, f(a) = 0.45.

There is a faster way to calculate the gene frequencies in a population than adding up the genes contributed by each genotype. Rather, you can use these handy formulae:

f(A) = f(AA) + f(Aa)/2

f(a) = f(aa) + f(Aa)/2

So, to calculate the frequency of a gene in a population, you add the frequency of homozygotes for that allele with 1/2 the frequency of heterozygotes. In our example, this would be:

f(A) = 0.35 + 0.4/2 = 0.35 + 0.2 = 0.55

f(a) = 0.25 + 0.4/2 = 0.25 + 0.2 = 0.45

Wow... that's a lot faster.

C. The Hardy-Weinberg Equilibrium Model

1. Goal:

The goal of the "Hardy-Weinberg Equilibrium Model" (HWE) is to describe what the genetic structure of the population would be if NO evolutionary change occurs. Working independently, Hardy and Weinberg realized that the gene frequencies in a population will NOT change - will remain in EQUILIBRIUM - if the following conditions are met:

- there is random mating

- no selection

- no mutation

- no migration

- and the population is infinitely large.

And, they realized that a population will reach an equilibrium in GENOTYPIC frequencies, too, after one generation of meeting these expectations. And, for as long as these conditions are met, a population will NOT EVOLVE. Let's see how they came by these conditions.

2. Example:

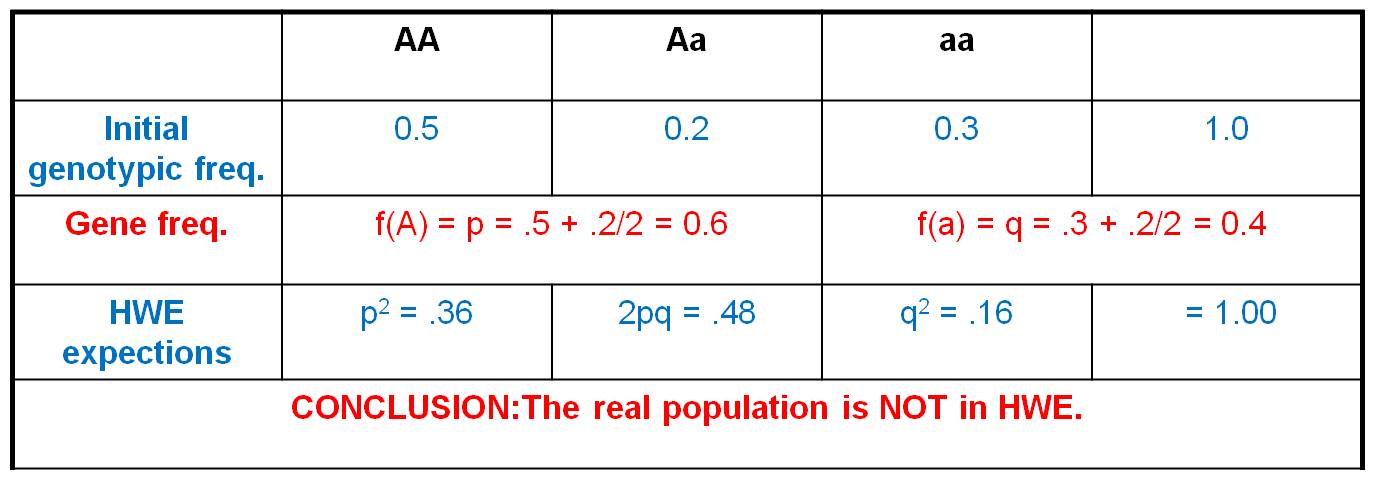
Consider an initial population, with a genotypic array as shown. The gene frequencies are:   

A = 0.4 + (0.4/2) = 0.6

a = 0.2 + (0.4/2) = 0.4                

Now, consider this gene pool in which 60% of the alleles are 'A' and 40% of the alleles are 'a' (as defined by the gene frequencies). The gene frequencies represent the frequencies of gametes carrying these gens; so 60% of sperm are 'A', 40% are 'a', and likewsie for eggs.

So, now we employ the HWE model. IF the population mates at random, then we can use the product rule to determine the probability of any two gametes coming together. The propability that and 'A' sperm fertilizes an 'A' egg = 0.6 x 0.6 = 0.36. And of course, this is the only way to produce an 'AA' zygote. The frequency of 'AA' zygotes (the F1 offspring) produced by this population should be 0.36. Likewise, the probability that an 'a' sperm fertilizes an 'a' egg = 0.4 x 0.4 = 0.16. And again, this is the only way to make an 'aa' zygote, so the total frequency of 'aa' zygotes in the F1 will be 0.16. Now, there are two ways to make an 'Aa' zygote: an 'A' sperm can fertilize an 'a' egg (probability = 0.6 x 0.4 = 0.24), and an 'a' sperm can fertilize an 'A' egg (also with a probability of 0.4 x 0.6 = 0.24). So, the total frequency of Aa zygotes in the F1 will be 2 x 0.24 = 0.48. If we generalize, and let f(A) = p and f(a) = q, then the genotypic frequencies under HWE can be calculated as: f(AA) = p², f(Aa) = 2pq, and f(aa) = q².

What is the genetic structure of the population in the F1? Well, f(A) = f(AA) + f(Aa)/2 = 0.36 + 0.48/2 = 0.36 + 0.24 = 0.6. And, f(a) = f(aa) + f(Aa)/2 = 0.16 + 0.48/2 = 0.4. So, the gene frequencies did not change. And, if these organisms produce gametes at these gene frequencies and mating is random, then F2 zygotes should be formed at the frequencies of f(AA) = 0.36, f(Aa) = 0.48, and f(aa) = 0.16. Look familiar? Indeed, after one generation of random mating, the population has reached an EQUILIBRIUM - constant gene and genotypic frequencies over time.

Now, of course, these calculations will only be true IF the population mates at random. AND, they will only be true if there is no mutation. If 'A' alleles are mutating into 'a' alleles, then the gene frequencies will not be 0.6 and 0.4, and calculations based on these numbers will not be correct. So, we must assume NO MUTATION. Likewise, we can't have any migration; we can't have 1000 AA individuals migrate into our population, or that would change the gene frequencies, too; and our predictions based on frequencies of 0.6 and 0.4 would be incorrect. So, we must assume NO MIGRATION, too.

So, at this point we have zygotes at the frequencies shown in the "Genotypes, F1" row. In order for there to be no change in the genetic structure of the population, there must be NO SELECTION. In other words, all genotypes must have the same probability of survival and reproduction. Only then will they contribute gametes at frequencies of p = 0.6 and q = 0.4. (If there were selection, and if AA individuals were the only zygotes to survive to reproduce, for instance, then the gene frequencies would change and our predictions based on frequencies of 0.6 and 0.4 would not be correct).

And finally, this model will only be explicitly true for populations that are infinitely large: because that is the only time when we can be garaunteed that predictions based on random chance will be exactly met. (Think about it this way... suppose I give you a coin that is absolutely perfectly balanced. It IS PERFECTLY BALANCED. And suppose I ask you, "how many times do you have to flip that coin to be ABSOLUTELY SURE of producing a 50:50 ratio of heads to tails? Well, if you only flip it four times, you know that, just by chance, you would often get 3 heads and a tail or 3 tails and a head. And even if you flip it 10,000 times, you might get 5001 heads and 4999 tails, even though the coin is perfectly balanced. To be absolutely garaunteed that the predictions of this probabilisitic model will be met exactly, you must flip the coin an infinite number of times. Obviously, this is a theoretical constraint because no population is infinitely large. But this is a theoretical model of no change, so we can employ theoretical expectations. The same is true of our 'expectation' of a perfectly balanced coin - this expectation will only be met, for sure, in an infinitely large sample. Yet we continually employ that expectation for a perfectly balanced coin, even in finite samples. So, if you flip the coin 20 times, how many heads would you expect? Your answer of 10 is a theoretical expectation.

So, that is why these assumptions exist. It is only when ALL these are met that the genetic structure of a population will not change. It is only when ALL these assumptions are met that a population will NOT evolve. Wow. That should seem rather amazing. It is only when these assumptions are ALL met that a population WON'T change. If any of these assumptions is not met, a population's genetic structure WILL change... and that is evolution. So, from this analysis, we should expect populations to evolve - it is only under a rare combination of events (no, mutation, no selection, no migration, random mating, and an infinitiely large population) that evolution WON'T happen.

3. Utility                

- If no real populations can explicitly meet these assumptions, how can the model be useful?  For instance, no real population is infinitely large, so how can the model be useful?  We use it for COMPARISON.  This model describes what the genotypic frequencies should be IF the population was in equilibrium.  If the real genotypic frequencies are not close to these expectations, then the population is not in HWE.... it is evolving. And if a population is not in HWE, then the population must be violating one of the assumptions of the HWE model.  Think about that.  The HWE is only 'true' if all the assumptions are being met.  If your real population differs from the model, then one of the assumptions must not apply to your real population.  This narrows your focus on WHY the real populations isn't behaving randomly... and it might identify WHY the population is evolving.... which is a biologically interesting question.                

- Again, the coin analogy applies.  No REAL coin is probably exactly perfectly balanced. But, if I give you a coin and ask you how balanced it is, you flip it a few times and compare its behavior to WHAT YOU WOULD EXPECT FROM A PERFECT COIN (50:50 RATIO). Even though a perfectly balanced coin may not exist, we can use this theoretical model as a benchmark, to compare the behavior of real coins.  Many real coins act in a manner that is consistent enough with the expectations from a perfectly balanced coin that we are willing to use them AS IF they were perfectly balanced.   The Hardy Weinberg Equilibrium Model is the same... it is a theoretical model of no change against which we can measure real populations. 

If HWE can be assumed, then the frequency of recessive diseases can be assumed to equal q², and the frequency of carriers in the population can be estimated like this:

1) The frequency of hemachromatosis worldwide is 1/450. If we assume that hemochromatosis is caused by a recessive gene (q), and if we assume the population is in HWE with respect to this trait, then q² = 1/450 = 0.002. So, we take the square-root of both sides to find q = 0.047. Well, if q = 0.047, and if p + q = 1, then p = 1 - 0.047 = 0.953.

2) If q = 0.047 and p = 0.953, then the frequency of heterozygous carriers = 2pq = 0.09. So, we estimate that 9% of the population are carriers.

Now, you might say, "but we just determined that HWE would be unusual; so why would we assume it is true for a given gene?" Well, a deleterious gene has already been largely weeded out of a population, so selection against the few alleles that are left is really weak. Indeed, this condition may not influence reproductive success, anyway (NO SELECTION). In addition, we don't select mates based on whether they have hemochromatosis (I bet you NEVER asked your date if they have hemochromatosis, for example!!), so we can assume there is RANDOM MATING in the population with respect to this trait. And although the human population is not infinite, it is really big (~7 BILLION), so the effect of sampling error is probably very small. Mutation is very rare, so the effects of mutation are likely to be very small. And if we are making an estimate based on the whole human population, then there can be no 'migrants' coming in from somewhere else (Martians?). So, in some cases, we can reasonably assume a population might be in HWE for a given gene. Of course, we could be wrong... and we would test that prediction by sampling individuals in the population and determining the frequency of heterozygotes genetically. But at least we would have a working hypothesis.

As we've seen, equilibrium can only occur if ALL of the assumptions are met. If they are not met, then the population will evolve. We are now going to look at each assumption, and consider what happens when each assumption is violated. This will show us how evolution can occur by each of these different agents of evolutionary change.

D.  Deviations From HWE:

1. Mutation

Although large scale mutations like polyploidy can cause instantaneous speciation, what we are talking about here are substitution mutations that change one allele into another, or make a new allele.   Although such changes are very important sources of new variation, they do not change the genetic structure of a population very much at all, even when they occur: these mutations are rare, usually occurring at a rate of 1 x 10^-4 to 1 x 10^-6.

Consider a population with:
f(A) = p = 0.6
f(a) = q = 0.4
Suppose 'a' mutates to 'A' at a realistic rate of: µ = 1 x 10^-5 . How will this rate of mutation change gene frequencies? Not much: 'a' will decline by: qm = .4 x 0.00001 = 0.000004
'A' will increase by the same amount. So, the new gene frequencies will be: p1 = p + µq = .600004, and q1 = q - µq = q(1-µ) = .399996. So, mutation is a very important source of new alleles, but it doesn't change the gene frequencies in a population very much.

2. Migration

Consider a resident population in which p = 0.6 and q = 0.4. Suppose immigrants migrate into this population, bringing A and a alleles into the population at these frequencies: p =0.8 and q = 0.2. The effect of this influx will depend on the number of immigrants relative to the number of residents. 100 immigrants may not change the genetic structure of a population containing 1 million residents, but they could have a dramatic effect on a population of 100 residents. We measure this relative effect by quantifying the proportion of the total combined population that are immigrants. So, in our example, suppose so many immigrants move in that they represent 10% of the new, combined population.  We calculate new p as a weighted average based on fraction of immigrants and residents:                        

So, p1 = (0.6)(0.9) + (0.8)(0.1) = 0.54 + 0.08 = 0.62
residents contribute p at a rate of 0.6, and they represent 90% of the combined population.  Immigrants contribute p at a rate of 0.8, and they are 10% of the population.
q1 = (0.4)(0.9) + (0.2)(0.1) = 0.36 + 0.02 = 0.38, so we have done our math right because 0.62 + 0.38 = 1.0

There are two possible evolutionary effects. First, migration will make two populations similar to one another; particularly if the rate of immigration is high or the process is continuous over time. Migration can also introduce new alleles into a population, but again this effect will be correlated with the abundance of immigrants relative to the number of residents.  

3. Non-Random Mating:            

a. Positive Assortative Mating

There are many ways that non-random mating can occur. We will look at a couple. The first example is called "positive assortative mating". This is where mates 'sort' themselves with others of the same genotype. This can be thought of as "like mates with like". So, consider our old four o'clock plants with incomplete dominance. A population might contain red, pink, and white flowers. Suppose the red flowers open in morning, and are pollinated just by hummingbirds (that prefer red flowers). Suppose the white flowers open at night, and are pollinated by moths. And suppose the pink flowers open in the afternoon, and are pollinated by bees and butterflies. In this case, "like mates with like" for flower color (and time of opening). So, a plant with red flowers will only mate with another plant having the same genotype for (red) flower color. Now, it is IMPORTANT to realize that plants are only positively assorting for flower color and opening time in this case. One red flowering plant may be tall while the other is short; one may have hairy leaves while the other has smooth leaves. Indeed, the plants may be mating at random with respect to all other traits.

When AA individuals mate only with each other, all their offspring will be AA, as well. So, if 20% of the population is AA (intial genotypic frequency = 0.2), and if there is no difference in reproductive success (because we are only violating the assumption of random mating so there is no selection), then these parents will make 20% of the offspring and they will all be AA. The same goes for aa individuals only mating with other aa individuals - all their offspring are aa. However, when Aa heterozygotes only mate with one another, they produce AA, Aa, and aa offspring in a 1/4:1/2:1/4 ratio. If 60% of the population is heterozygous, then they will make 60% of the offspring... but these offspring won't all be heterozygous; only 1/2 - or 30% will be heterozygous. 15% will be AA and 15% will be aa. So, the total frequency of AA offspring in the F1 will be 35%; 20% had AA parents and 15% had Aa parents.

As a consequence of positive assortative mating, the frequency of heterozygotes will decline and the frequency of homozygotes will increase. Curiously, the gene frequencies won't change, so in the F1, f(A) = .35 + 0.30/2 = 0.5... just as it was in the orginal population (f(A) = 0.2 + 0.6/2 = 0.5). The genes are just being 'dealt' to offspring in a non-random manner, affecting the genotypic frequencies at this locus.

So, suppose we observed the F1 population in nature, and wanted to know if it was in HWE. We would calculate the gene frequencies (A = 0.5, a = 0.5), and then estimate what the frequencies of the genotypes would be IF the population was in HWE: p² = 0.25, 2pq = 0.5, q² = 0.25. We would compare our real population's genotypic array with this HWE expectation, and see that they are not the same. And we could see one thing more... we would see that the ACTUAL OBSERVED frequency of heterozygotes (0.30) is LESS THAN the expected frequency of heterozygotes under the HWE hypothesis (0.5). And we would see that the observed frequency of both homozygotes is greater than expected. Knowing that positive assortative mating can cause this pattern, we would have a working hypothesis regarding the agent of evolution at work in this population.

b. Inbreeding: Mating with a Relative

Inbreeding is mating with a relative. It is similar to positive assortative mating, except that the two mates are not just similar at one locus, but they are probably similar at MANY loci because they are related and got their genes from the same ancestors. Siblings share, on average, half their genes. Matings between siblings, then, will tend to reduce heterozygosity at MANY loci, not just one.

The most extreme example is "obligate self-fertilization". This is where a hermaphrodite ONLY mates with themselves. This is not asexual reproduction - they produce gametes by meiosis and get all the benefits of producing variable gametes that occurs in sexual reproduction; but they only fertilize their own gametes. This has a profound effect on the genetic structure of the population. Think about it: when an organism mates with themselves, they are mating with an organism that has the SAME genotype at EVERY locus. So, there will be a decrease in heterozygosity across the entire genome, with a 50% reduction in heterozygosity each generation. This is the most rapid loss possible. Siblings are only related, on average, by 50%, so the loss of heterozygosity will only occur 1/2 as fast.... but it will still occur at all loci across the genome.

Inbreeding often reduces reproductive success, because there is an increase in homozygosity - and this means that deleterious recessives are going to be expressed more frequently and exert their negative effects on the offspring. A deleterious allele may be rare in a population, but inbreeding will increase the probability that it occurs in the homozygous condition and is expressed. Because inbreeding can reduce the survivorship of offspring and thus reduce reproductive success of the parent, it is often selected against. Selection favors different strategies that reduce the likelihood of inbreeding, like "self-incompatibility" in some plants, like lions who push male cubs out of a pride when they mature (thus they don't breed with their sisters), or like humans who have a variety of cultural taboos against breeding with relatives.  However, inbreeding is also a mechanism for purging deleterious alleles from the population.  If a population can get through the first few generations in which homozygote recessive are produced and selected against, the net effect will be to eliminate these deleterious alleles from the population.  That can be a good thing in the long run.
 
  Things to Know:

1.  What are the five assumptions of the Hardy-Weinberg Equilibrium Model?

Study Questions:

1.  Consider the following population:

• - calculate the genotypic frequencies.
• - calculate the gene frequencies
• - calculate the HARDY WEINBERG EQUILIBRIUM frequencies.

2. If the HWE model does not describe any real population, how can it be useful?

  Study Questions:

3. Consider a population with p = 0.8 and q = 0.2. If the mutation rate of A--> a = 4.0 x 10^-6, what will the new gene frequencies be in the next generation?

4. Consider a population, p = 0.8 and q = 0.2. If migrants enter this population with p = 0.1 and q = 0.9, such that immigrants comprise 15% of the total population, what will the new gene frequencies be?

5. If the population below undergoes positive assortative mating, what will the genotype frequencies be in the next generation?